Recommendation Algorithms

Advantage: Efficient and effective. Usage: Recommendation Systems

Collaborative Filtering

User-based filtering

向用户推荐与他相似的用户感兴趣的物品。

基本步骤：

• 计算用户之间的相似度
• 根据相似度对用户进行评分
• 找到相似用户集合中其他用户感兴趣但是从未出现在该用户列表中的物品，推荐给该用户

1. 相似度计算方法

   1. 余弦相似度，Cosine similarity 给定两个向量$A,B$，余弦相似性有点积和向量长度给出

      \[\begin{equation} \text{similarity} = \cos(\theta) = \frac{A^\top \cdot B}{\parallel A \parallel \times \parallel B \parallel} \end{equation}\]

      Code:

       def cosSimi():
           rg = np.random.default_rng(1)
           a = rg.random((1, 10))
           b = rg.random((10, 1))
           cosSim = np.dot(a, b) / (nl.norm(a) * nl.norm(b))
           print(cosSim)
      

   2. 杰卡德相似度，Jaccard Similarity 给定两个集合$A, B$，定义为

      \[\begin{equation}\text{J(A, B)} = \frac{| A \bigcap B |}{ | A \bigcup B |} = \frac{|A\bigcap B|}{|A+B| - |A\bigcup B|}\end{equation}\]

      经常用户one-hot向量的相似度计算。

      code：

       def jaccardSimi():
         a = np.random.randint(0, 2, 15)
         b = np.random.randint(0, 2, 15)
              
         intersection = np.logical_and(a, b)
         union = np.logical_or(a, b)
         return intersection.sum() / float(union.sum())
      

2. 利用相似度进行评分

   1. 相似度评分

      \[\begin{equation} r(u, i) = \sum_{v \in S(u) \bigcap N(i)} w_{uv} r_{vi} \end{equation}\]

      其中，$r(u, i)$是用户$u$对物品$i$的评分，$S(u)$为到用户$u$最近的所有用户的集合，$w_{uv}$为两个用户之间的相似度，$r_{vi}$表示用户$v$对物品$i$的评分，$N(i)$为对物品$i$操作过的用户集合。

Item-based Filtering

向用户推荐他们以前喜欢的物品的相似物品。

• 计算物品之间的相似度
• 选出最相似的n个物品
• 根据相似度计算用户评分

1. 物品相似度计算公式

   \[\begin{equation} w_{ij} = \frac{| N(i) \bigcap N(j) |}{|N(i)|} \end{equation}\]

   其中，$w_{ij}$是连个物品之间的相似度，$N(i)$是喜欢物品$i$的用户集合，$N(j)$是喜欢物品$j$的用户集合，同时喜欢两个物品的用户数量占只喜欢物品$i$的用户数量的比例。

   但是由于热门物品的相似度和每个都会非常高，改进后的计算公式为：

   \[\begin{equation}w_{ij} = \frac{| N(i) \bigcap N(j) |}{ \sqrt {| N(i)| \cdot |N(j)|}} \end{equation}\]

2. 相似度评分计算 参见上一部分 https://www.notion.so/Recommendation-Algorithms-1353701a5f8b436a81fa4bea2fb52134#ffddb8aa36dd49609848cddfc8fbf0be

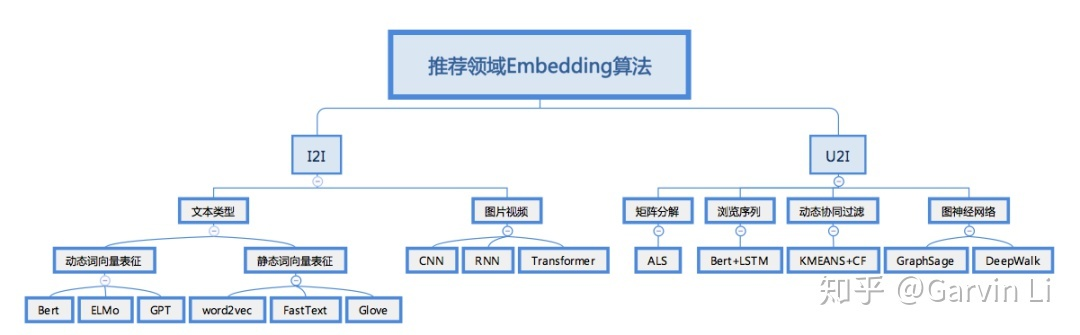
Embedding Based Algorithms

Embedding I2I