好的模型都是类似的,差的模型各有各的不幸
- 时间:2024.05.13
- 作者团队:MIT
- 作者:Minyoung Huh, Brian Cheung, TongzhouWang, Phillip Isola
- 有用指数:⭐️⭐️⭐️⭐️⭐️
- 贡献程度:⭐️⭐️⭐️⭐️⭐️
- 简单评价:用一个简洁的假设解释了很多问题,也预测了一些趋势,其中不乏较为详实的说明和严谨的推论。对于还在疑惑为什么大模型可以work的朋友,是一个很好的知识补充。
出发点
科学的发展总是基于一些可证伪的假设的证明或推翻,例如经典力学解释不了的现象,在微观粒度会有量子力学的理论进行支撑。某些看似不可能改变的理论,也仅在某些时空维度下是成立的。这篇文章就提出了一个假设,即,好的大模型的表征是正在收敛的,包括不同模态的模型。
作者试图用以下流程证明这个假设
- 不同大模型表征底层数据的方式正在逐渐对齐;
- 不同模态下,大模型衡量数据点距离的方法是非常相似的;
- 这个收敛的方向,是向着一个通用的现实统计学模型。
该假设的具象理解,假设现实是Z,那么X和Y两个模态的模型学习出来的embedding表征的内容是一致的。

如何证明这个表征是收敛的
作者只讨论可以产出embedding的模型。这里作者引入了一个kernel的概念。简单理解为模型区隔data points的本质特征,其实就是embedding。随后采用了mutual nearest-neighbor metric,用来衡量两个kernel之间的距离。作者试图证明两个东西
- 不同的神经网络正在收敛;
- 收敛的这个现象在不同的模态下都是成立的。
mutual nearest-neighbor metric(MNNM)方法简单来说,就是把图文Pair$(x_i, y_i) \in \mathcal{X}$ 用不同模态的模型分别Encode成各自模态下的embedding,再把每一个mini-batch下的embedding进行聚类,看每个sample聚类出来的结果交集作为该Metrics衡量指标。例如,有图文对(1,a), (2, b), (3, c),分别用LM处理123,Vision处理abc,处理完的embedding进行KNN聚类,1和2的距离和a与b的距离更接近,则表示两个kernel的距离更近。
他们介绍了一个工作,叫做model stitching(模型缝合)。给定两个训练好的模型$f$和$g$,假设他们都是由n层神经网络组成的,作者引入一个仿射层h,组成一个新的网络
\[\begin{equation} F = f_1 \circ \cdots \circ f_k \circ h \circ g_{k+1} \circ \cdots \circ g_m \end{equation}\]如果这个新的网络$F$能有很好的表现,那么就证明$f$和$g$有能兼容的层。
他们的实验结果共有两个发现,
- 一个在ImageNet上训练的视觉网络能和一个在Places-365上训练的网络进行对齐并保持较好的表现;
- 更靠前的层比靠后的层可交换性更强。
作者找了一共78个Vision Model,在VTAB数据集上做了实验,得到了如下结果:表现优秀的模型聚类都在一起,表现差的模型都分布在不同的地方。
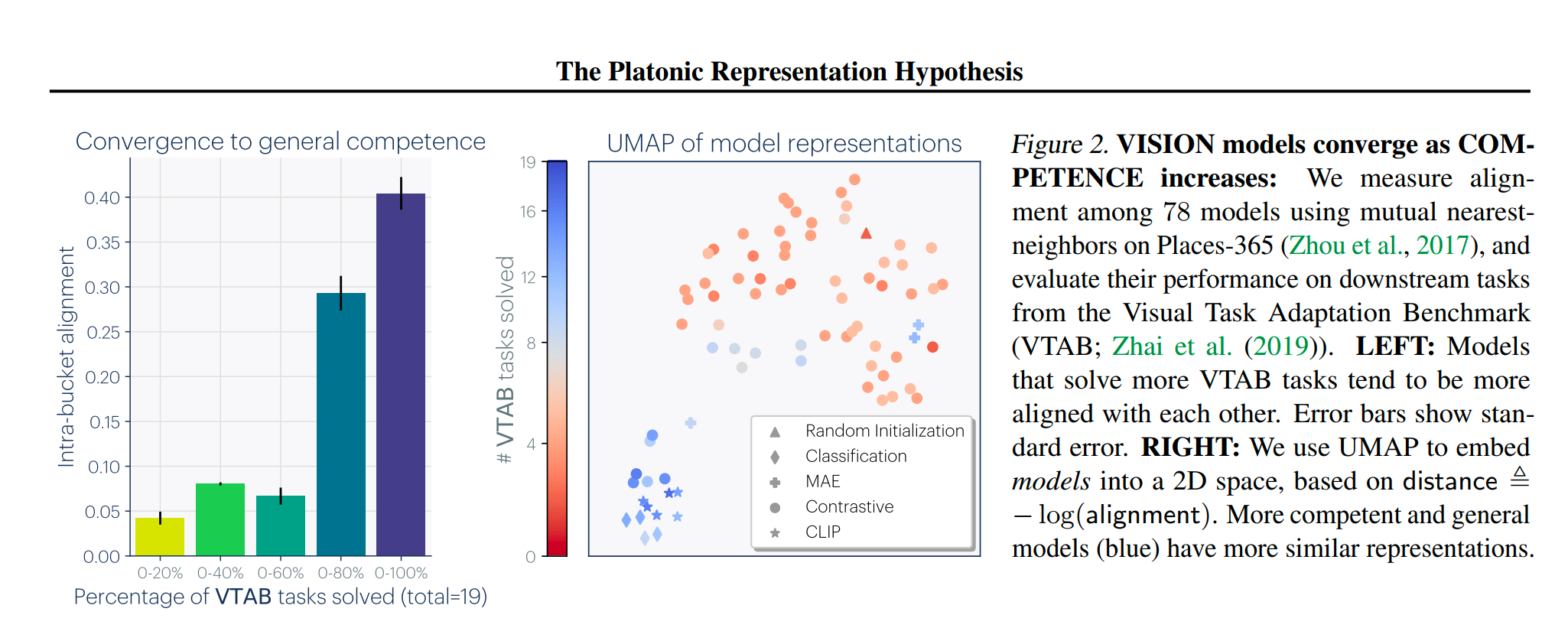
echo一下开头的结论:好的模型都是相似的,差的模型各有各的不幸。
模型参数也是收敛的吗?
简单的答案是:能。作者没有展开讲,但有几个工作发现对于不同的参数空间,它们倾向于向某一个地方进行收敛。
不同模态之间特征也是收敛的吗?
答案:是。有很多现象可以证明,例如LLaVA等多模态架构,仅用一个简单的Projector就能连接两个不同模态的大模型。更加能证明此处的一点是,参考BLIP-2的模型架构,它本质只做了prefix-tuning,没有更新LM的参数,就能够让LM识别图像特征。在语音领域同样有类似的现象。在下面的图里,图像或者语言模块的能力更强,两个模态能对齐的效果就越好,成本就越低。
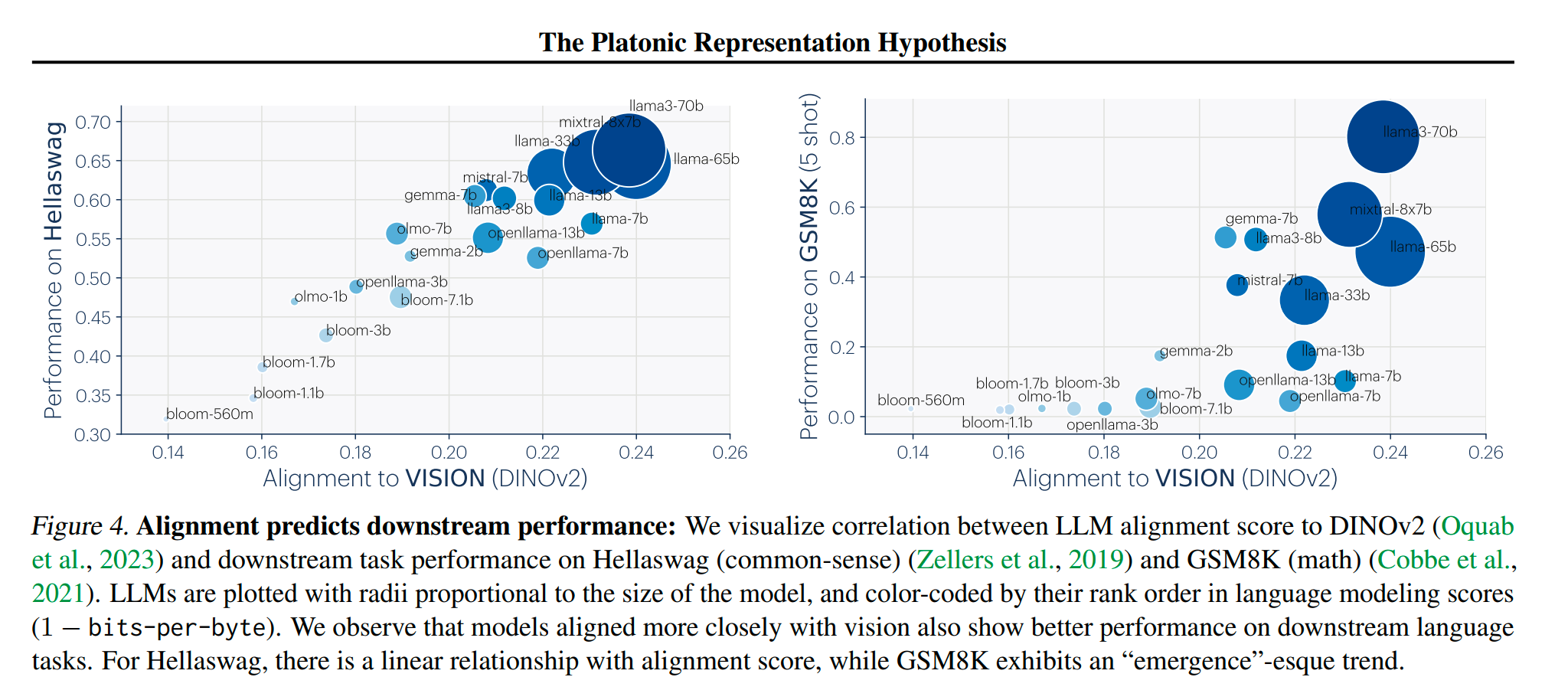
为什么表征在收敛
我们从模型参数的本质入手,模型训练的本质是降低训练集的经验风险的参数集合+正则化。

因此,从以下几点进行切入
从任务泛化性入手
我们把解决任务的方法想象成一个集合,对于任务A来说,可能有N种方法解决问题,对任务B来说,有M种方法可以解决问题。所以对于一个可同时解决任务A和B的模型,这个方法是M和N的交集才能同时解决这两个问题。假设我们需要实现的任务越多,训练集越大,那么同时能解决这些问题的方法越少。
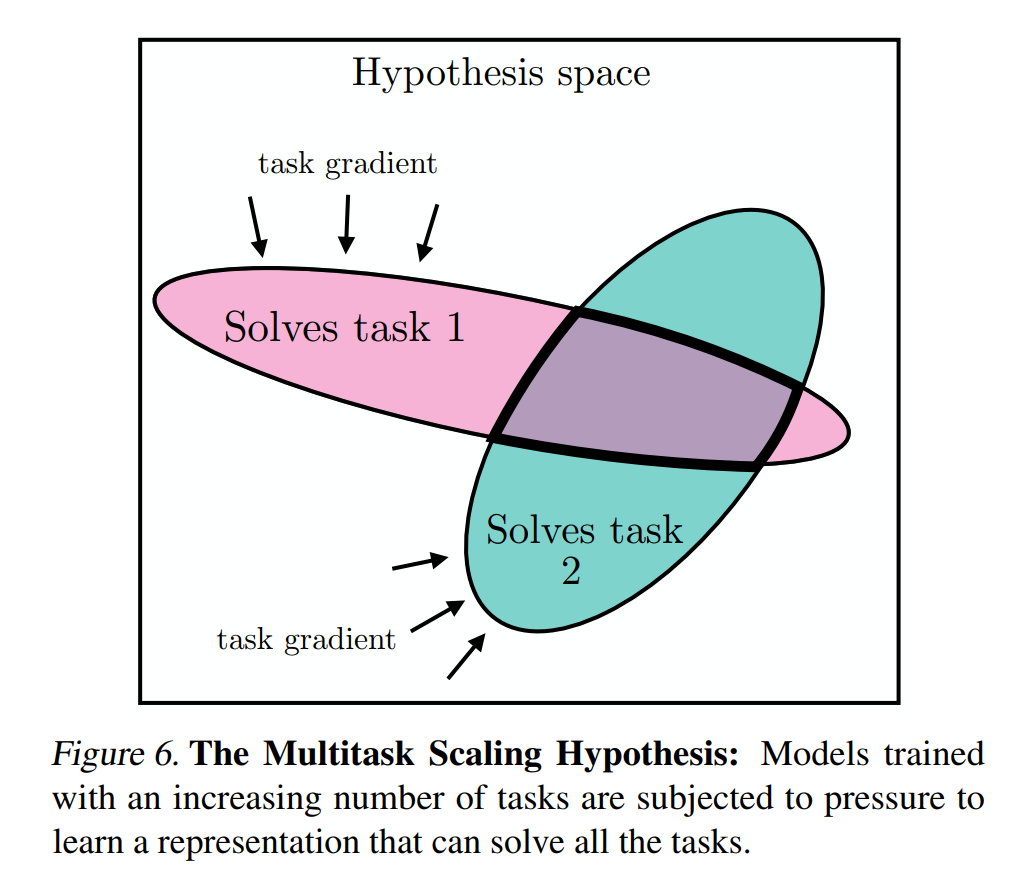
从模型容量入手
越大的模型参数空间越大,那么这个模型能够探索的空间也就越大,能力也就越强。
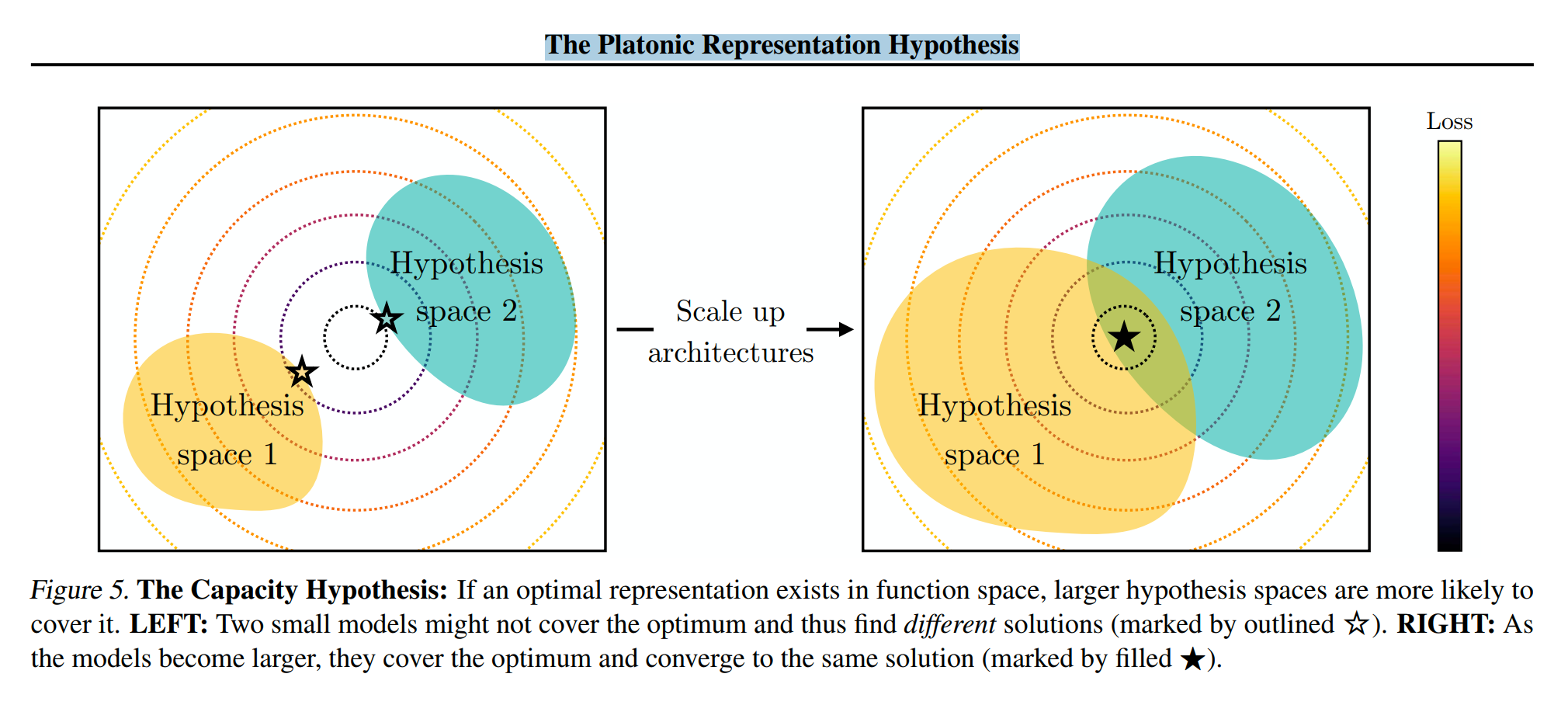
从Simplicity Bias思考
模型在对数据集进行拟合的时候,是什么导致了让模型不至于学习到特别复杂的表征呢?答案很可能是Simplicity bias。简单来说,在学习过程中,模型会”偷懒“,故意选择最简单能完成任务的方式。所以,根据这个假设,如果一个大模型在不同的数据集上训练过,那么结果可能会向更小的解法空间收敛。(这同时也是奥卡姆剃刀原则的一个直接延伸版本。
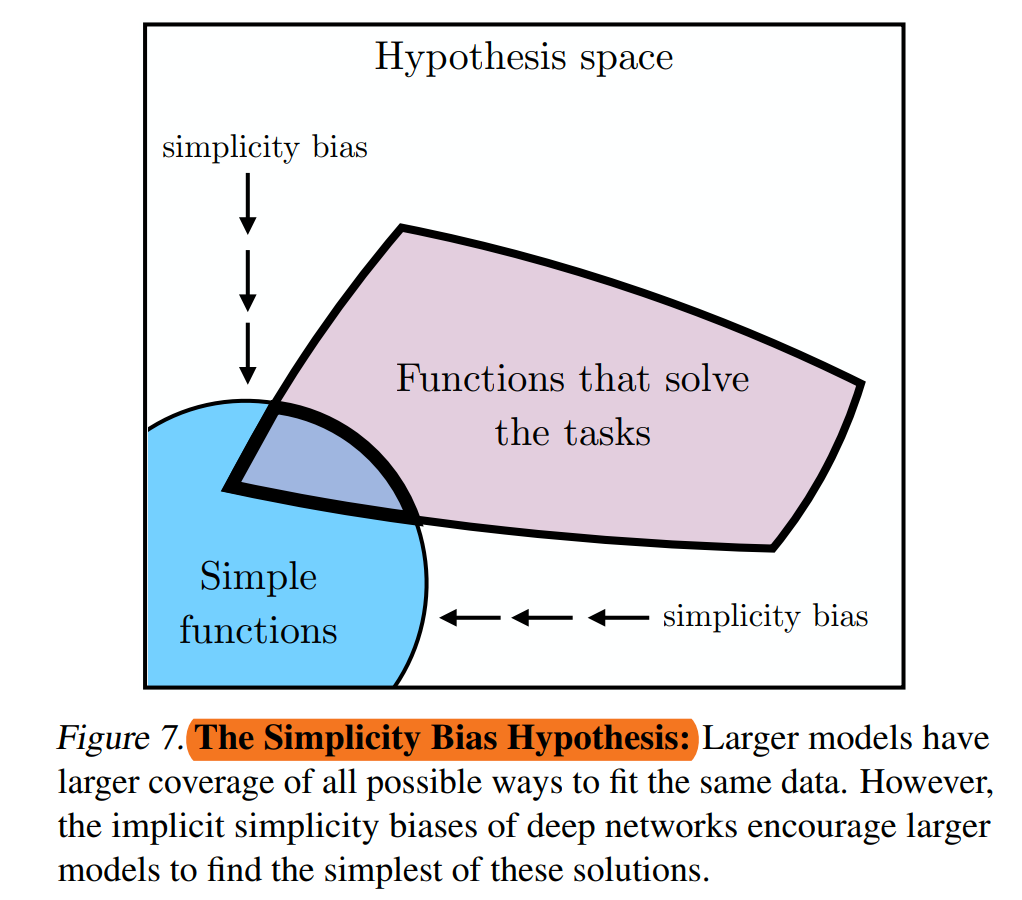
这个表征到底会收敛在何处?
一个简单的结论是:表征会收敛于离散事件在真实世界的点互信息kernel。
打个比方,”猫“和”喵“作为两个数据点,经过一个好的大模型的kernel,得到的两个表征,他们的点互信息(Pointwise Mutual Information)应该是接近真实世界的这个数值。因为这是两个事件的点互信息,所以这个方程是可适用于所有模态,甚至是跨模态的。比如文本模态:”猫在叫“和一个视觉模态:”视频中猫在真实的叫“,这两个数据的点互信息应该是比较大的(和现实比较接近)。
两个事件的互信息概率分布定义
\[\begin{equation} P_{\text{coor}}(x_a, x_b) \propto \sum_{(t, t') : |t - t'| \leq T_{\text{window}}} \mathbb{P}(X_t = x_a, X_{t'} = x_b). \end{equation}\]则两个表征之间的距离可以由以下公式计算
\[\left\langle f_X(x_a), f_X(x_b) \right\rangle \approx \log \frac{\mathbb{P}(\text{pos} \mid x_a, x_b)}{\mathbb{P}(\text{neg} \mid x_a, x_b)} + \tilde{c}_X(x_a) \\ = \log \frac{P_{\text{coor}}(x_a \mid x_b)}{P_{\text{coor}}(x_a)} + c_X(x_a) \\ = K_{\text{PMI}}(x_a, x_b) + c_X(x_a)\]既然我们假设了一个好的大模型是真实世界的映射,因此实际上kernel的点互信息就是真实世界的点互信息。
知道了表征收敛,有什么基于此的推论?
- Scaling是适用的,但不同方向的Scale有效率之分
- Scaling law告诉我们,模型的表现随参数量,数据集大小和算力之间都有正相关,但是Scale的效率在不同阶段有不同表现。比如,数据集质量是明显短板时(例如不同模态之间的丰富程度不同),Scale数据集质量要比Scale算力重要得多。
- 不同模态之间的数据集是可以共享的
- 如果你有N张图片和M条语料,又有假设是不同模态都可以反映现实,那么我们应该把图片数据和文本数据全部拿来训练。但他们之间可能有个换算关系,比如a个token代表b个pixels,少于这个关系可能无法作为可用训练的数据。
- 模态对齐在好的大模型之间应该是相当简单的函数
- 如果不同模态下,优秀的大模型有相似的底层表征,那么用尽可能简单的结构就可以把他们连接起来。
这个假设的缺陷在哪里?
- 有些东西只能用其固有模态表述。例如文本模态下根本不可能详细描述一张图片的所有细节,此时该假设为何成立?
- 作者argue的是,他们认同这个观点,但他们的假设比较严格建立在信息可严格双向映射情况,否则只能得到被其模态所能表达信息上限所限制的内容。
- 除了视觉和文本模态之外,很多模态并没有呈现出一种收敛的趋势
- 这里作者想了可能的原因,比如还没有探索如此深入等。
- 证明不同模型对齐能力的计算方法只能证明他们是相似的,但并不能证明是收敛的,更无法说明那个方向就是现实
- 这个是我提的,我自己的思考是,大语言模型用的很多数据集都是相同的,模型表现也是十分接近的,因此非常有可能只是模型相似,但并非都收敛到什么位置了。一切都是数据导致的。我对此的判断是(在物理学中很普遍的一个流程),我们可以先接受一个比较好的假设,这个假设用简洁的方程能解释很多问题,也能预测很多现象,在相当长的一段时间,如果该假设都能无法被证伪,那么我们可以先接受这个作为公理,直到有打破该公理的现象被观测到。