RoPE - 扩展context长度的利器
- 标题:RoFormer: Enhanced Transformer with Rotary Position Embedding
- 时间:2021.4.20
- 作者团队:追一科技,现在已经快倒闭了,只做NLP的一家公司
- 作者:Jianlin Su, Yu Lu, Shengfeng Pan, Ahmed Murtadha, Bo Wen, Yunfeng Liu
- 有用指数:⭐️⭐️⭐️⭐️⭐️
- 贡献程度:⭐️⭐️⭐️⭐️⭐️
- 简单评价:用旋转矩阵做了相对位置编码,从而提升了模型的外推性。
知识前提
大模型的Transformer架构中,是通过Positional Embedding的方法来保证模型能理解输入tokens之间的位置关系,一般都是在token转化为embedding之后,进入Multi-head attention之前会处理的操作。
一般来说,位置编码方法会影响到模型的==外推性==。即在短序列上训练的模型,能否扩展到长序列上面。
做Positional embedding的方法有两种
- 绝对位置编码(absolute positional embedding):考虑tokens之间的绝对位置
- 相对位置编码(relative positional embedding):考虑tokens之间的相对位置,一般来说会有$i-j$来表示两个tokens之间的相对距离。RoPE方法是这个大类里面的。
根据大量实验证明,相对位置编码要优于绝对位置编码,但是相对较好的RoPE也只能保持外推10%-20%而性能并不衰减,再多就也不行了。首先它相对于绝对位置编码有较好的外推性能是容易理解的,假如训练用的512的长度,推理用到了1024,绝对位置可能就不work了,但是相对距离对于第1023位置的token,还是能感知到511位置的token。
Existing Gap
在Transformer模型中,模型理解不同tokens之间距离和位置关系的方法是absolute positional embedding,简单来说就是对QKV矩阵中的embedding加上一个positional的embedding,而这个embedding是和位置有关系的。
绝对位置编码
公式$\eqref{abs_embed}$就是原始矩阵加上abs embedding之后的结果。
\[f_{t : t \in \{q, k, v\}} \left( \mathbf{x}_i, i \right) := \mathbf{W}_{t : t \in \{q, k, v\}} \left( \mathbf{x}_i + \mathbf{p}_i \right) \label{abs_embed}\]$p_i$是和输入相同维度的embedding。那$p_i$如何生成呢,之前一直是使用sinusoidal函数
\[\begin{equation} \begin{cases} p_{i, 2t} = \sin\left(\frac{k}{10000^{2t/d}}\right) \\ p_{i, 2t+1} = \cos\left(\frac{k}{10000^{2t/d}}\right) \end{cases} \end{equation}\]相对位置编码
在公式$\eqref{rel_emb}$中,相对位置编码改成了tokens之间的相对距离,距离用这个表示:$r = \text{clip}(m - n, r_{\min}, r_{\max})$。
\[\begin{equation} \label{rel_emb} \begin{aligned} f_q(x_m) &:= \mathbf{W}_q \mathbf{x}_m, \\ f_k(x_n, n) &:= \mathbf{W}_k (\mathbf{x}_n + \tilde{\mathbf{p}}_r^k), \\ f_v(x_n, n) &:= \mathbf{W}_v (\mathbf{x}_n + \tilde{\mathbf{p}}_r^v). \end{aligned} \end{equation}\]传统的相对位置编码和绝对位置编码各有什么缺陷?
- 绝对位置编码不能达成外推的目标;
- 相对位置编码需要计算pair-wise distance,所以相对位置编码的matrix大小是(T, 2T-1)
所以作者的问题变成了,如何能找到一个高效的方法,让两个word embedding相乘的时候,能够考虑到相对的位置信息,把这个问题抽象成函数表达,就是公式$\eqref{rel_func}$。
\[\left\langle f_q(x_m, m), f_k(x_n, n) \right\rangle = g(x_m, x_n, m - n). \label{rel_func}\]RoPE方法描述
作者是从二维的几何性质推导到多维,通过欧拉变换和三角函数等公式讲解的,比较晦涩难懂。任何数学==推导的目标==都及其重要,不然根本看不懂。这里作者的目标是,==找到能够代表公式$\eqref{rel_func}$的矩阵运算==。正向的过程是从向量变换开始思考,在二维空间内,找到$m-n$的表达方式。但这里由于我们已经知道作者使用了旋转矩阵,我们可以从旋转矩阵的定义和性质出发进行以下推导。
- 旋转矩阵的性质
假设$R_a$是角度为$a$的旋转矩阵,那么,
- ${R_a}^T={R_a}^{-1}$。(转置等于其逆)
- $\left\langle R_a, R_b \right\rangle = R(a+b)$
作者想证明的问题本质变成了$\left\langle R_aX, R_bY \right\rangle = \left\langle X, R_{(a-b)}Y \right\rangle$。
证明过程如下
\[<RaX, RbY>\\ =(RaX)^T RbY \\ =X^T Ra^T RbY \\ = X^T R(b-a) Y \\ = <X, R(b-a)Y>\]也因此,可以直接使用一个旋转矩阵来做相对位置编码。
总结
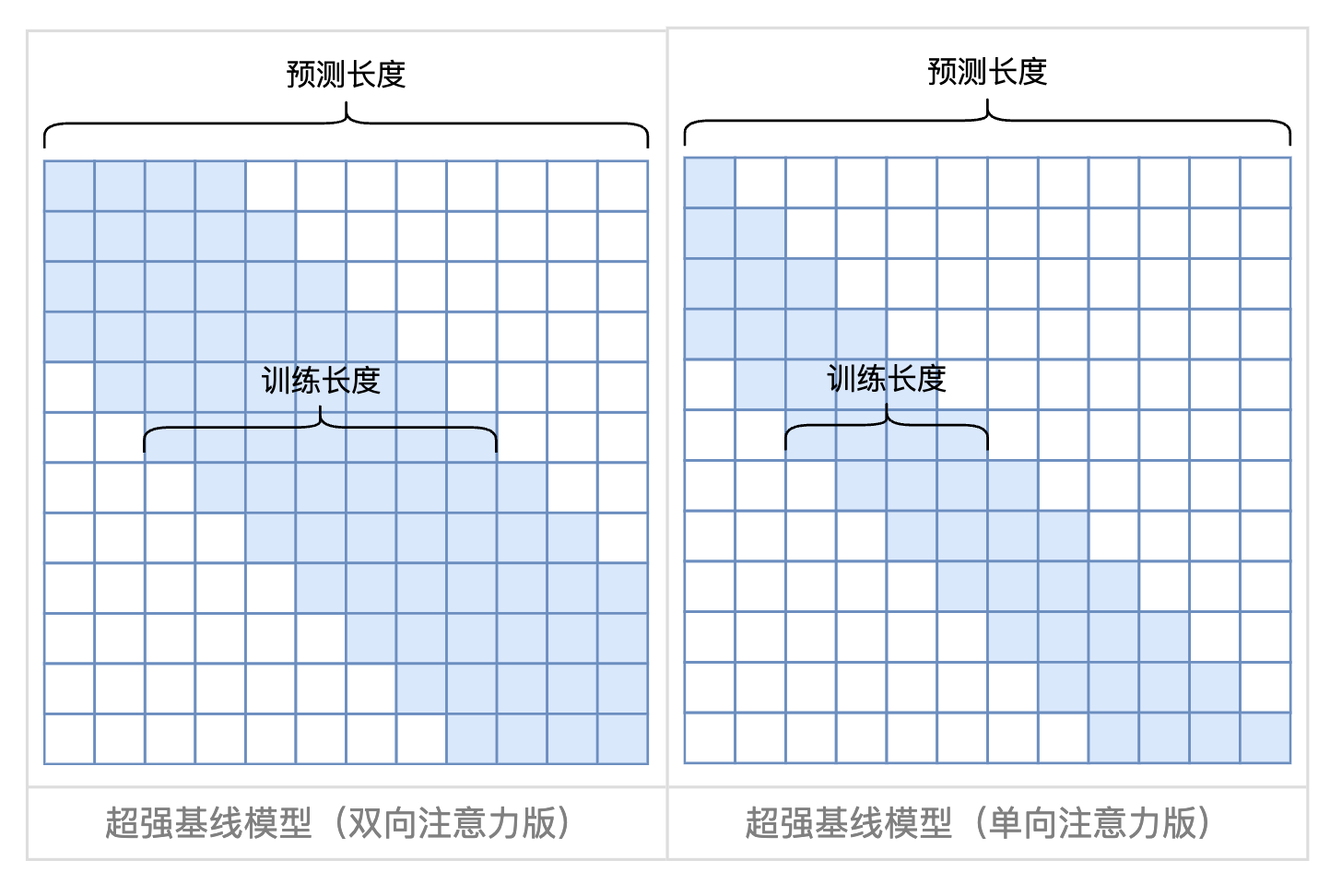
推荐一篇思考比较深入的文章,对训练和推理长度不一致的外推有很深入的思考。简单来说,只要在推理的时候使用一个简单的attention mask,就能通过local attention来很好实现接近于SOTA效果的外推。https://spaces.ac.cn/archives/9431/comment-page-1#mjx-eqn-eq%3Aalibi