Chengru's Blog

【AI】Reinforcement Learning

 
  • 2023年 10月06日

Reference

  1. Key concepts

    A (Long) Peek into Reinforcement Learning

  2. Policy Gradient

    Policy Gradient Algorithms

Key Concepts

What

定义

The agent’s policy $\pi(s)$ provides the guideline on what is the optimal action to take in a certain state with the goal to maximize the total rewards.

关键词，在某个state下，采取何种策略，能够让rewards的总和最大。

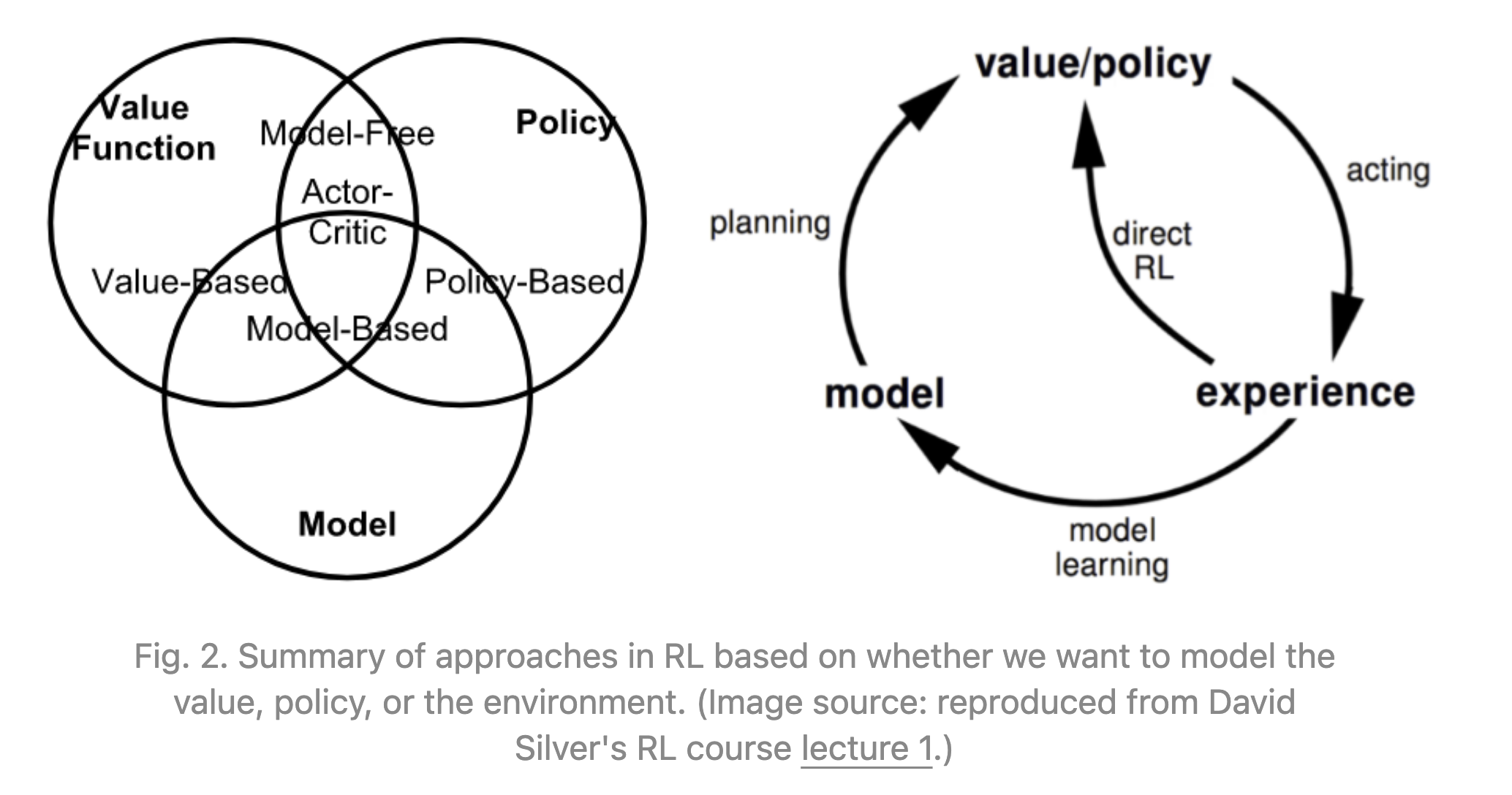
image-20231006173349512

Model

模型就是对环境的一种描述，这种描述能够告诉参与者在当前状态下可采取的行动有哪些。主要由Transition probability function $P$ 和Reward function $R$ 组成。

Reward function $R$，预测被Action trigger后的下一次的Reward。

\[R(s, a)=\mathbb{E}\left[R_{t+1} \mid S_t=s, A_t=a\right]=\sum_{r \in \mathcal{R}} r \sum_{s^{\prime} \in \mathcal{S}} P\left(s^{\prime}, r \mid s, a\right)\]

Transition Function $P$，定义在采取某个Action的情况下，State的变化规律。

\[P_{s s^{\prime}}^a=P\left(s^{\prime} \mid s, a\right)=\mathbb{P}\left[S_{t+1}=s^{\prime} \mid S_t=s, A_t=a\right]=\sum_{r \in \mathcal{R}} P\left(s^{\prime}, r \mid s, a\right)\]

Policy

Policy就是行为描述函数，在某个状态 $s$ 下，需要采取何种策略。

  1. 确定性Policy：$\pi(s) = a$
  2. Stochastic Policy: $\pi(s) = \mathbb{P}[A = a \mid S = s]$

Value Function

通过对未来Reward的预测，来评价当前的state有多么rewarding。

\[G_t=R_{t+1}+\gamma R_{t+2}+\cdots=\sum_{k=0}^{\infty} \gamma^k R_{t+k+1}\]

$\gamma$ 是打折系数，这个系数在0~1之间，因为

  1. 未来的Reward是预测的，且可能不准；
  2. 未来的Reward无法提供及时反馈；
  3. 未来Reward需要无限tracking。

State value: 在State s时，可以获得的return。 \(V_\pi(s)=\mathbb{E}_\pi\left[G_t \mid S_t=s\right]\)

Action Value：在某一个State下面采取某种Action所能得到的Value。也叫做Q-value \(Q_\pi(s, a)=\mathbb{E}_\pi\left[G_t \mid S_t=s, A_t=a\right]\)

除此之外，因为我们有某种策略$\pi$，因此我们可以通过策略和Action Value来计算得到State Value。

\[V_\pi(s)=\sum_{a \in \mathcal{A}} Q_\pi(s, a) \pi(a \mid s)\]

还有一个定义叫做A-value，就是Advantage Value，是Action Value和State Value之间的差值，可以理解为采取某一个Action之后能比现在的State Value带来多少增益。

\[A_{\pi}(s, a) = Q_{\pi}(s, a) - V_{\pi}(s)\]

Optimal Value & Policy

这就非常直白了，Optimal Value能够提供最大的Return，看公式$\eqref{op_v}$

\[V_*(s)=\max _\pi V_\pi(s), Q_*(s, a)=\max _\pi Q_\pi(s, a) \label{op_v}\]

与此相对应的最优策略可以表达为

\[\pi_*=\arg \max _\pi V_\pi(s), \pi_*=\arg \max _\pi Q_\pi(s, a)\]

这两者是否有冲突呢？

没有，因为最优策略就是Value function最大的时候的策略值。

Learning Type

machine learning - What is the difference between policy-based, on-policy, value-based, off-policy, model-free and model-based? - Cross Validated (stackexchange.com)

  • On-policy v.s. Off-policy: 核心区别在于学习时，如何更新Q-value。
    • Off-Policy会在每个Action后采取最好的Action来更新$Q(s,a)$，
    • 而On-Policy会用当前策略更新$Q(s,a)$。
  • Policy-based v.s. Value-based:
    • Value-based: 先学习Value function，再根据这个Value function来学习最优策略.
    • Policy-based：显式学习一个Policy的representation，mapping $ \pi: s -> a$，这个mapping关系是存储在内存中的。
    • Actor-critic：是以上两者的混合。
    • 本质区别：Value指的是给定State $s_t$ 和动作$a_t$，可以获得累积奖励的期望值，因此这是一个更注重于未来收益最大化的衡量方式；Policy指的是，找到策略$\pi_t$，使得累积奖励的期望值最大化。

Markov Process

RL问题都可以看成一个Markov decision Process，MDP将问题简化为，所有未来的状态，都有且只与当前状态有关，历史状态都已经被encode到当前状态下了。

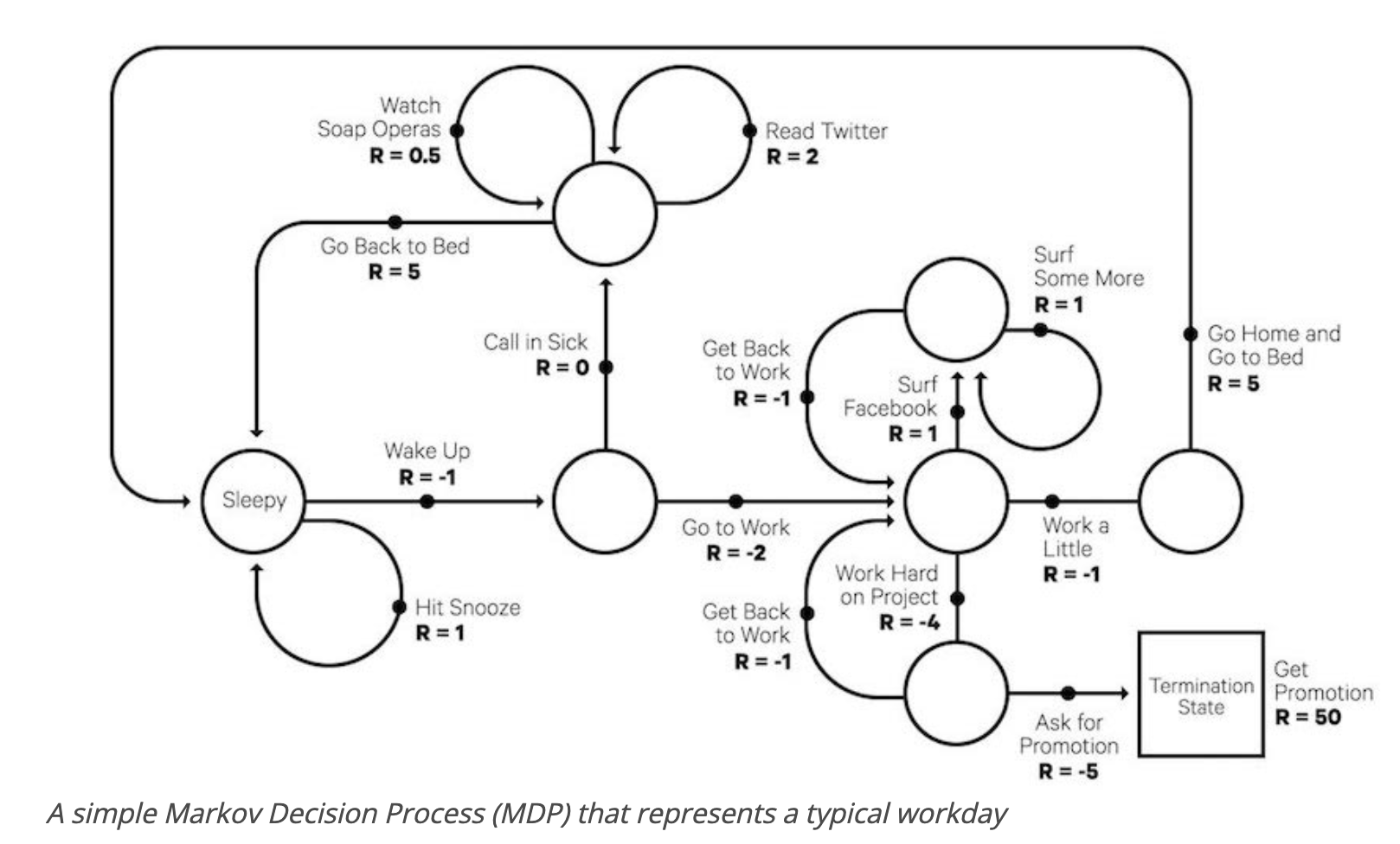
image-20231007144448641

注意一下公式$\eqref{eq_bellman}$，如果我们想直接获得最优解而不是策略，我们其实不需要考虑策略$\pi$，而是直接根据状态转移矩阵计算Q-value和State Value。

\[\begin{aligned} V_*(s) & =\max _{a \in \mathcal{A}} Q_*(s, a) \\ Q_*(s, a) & =R(s, a)+\gamma \sum_{s^{\prime} \in \mathcal{S}} P_{s s^{\prime}}^a V_*\left(s^{\prime}\right) \\ V_*(s) & =\max _{a \in \mathcal{A}}\left(R(s, a)+\gamma \sum_{s^{\prime} \in \mathcal{S}} P_{s s^{\prime}}^a V_*\left(s^{\prime}\right)\right) \\ Q_*(s, a) & =R(s, a)+\gamma \sum_{s^{\prime} \in \mathcal{S}} P_{s s^{\prime}}^a \max _{a^{\prime} \in \mathcal{A}} Q_*\left(s^{\prime}, a^{\prime}\right) \end{aligned} \label{eq_bellman}\]

Solutions

解决问题的目标：习得一个能够最大化未来Reward的Policy。

明确几个问题

  1. Episode和Action的区别：一个episode是一系列actions和states的组合，一个episode表示一个学习周期已经结束，达到了既定目标。一个Action仅表示一个动作。

Monte Carlo Method

  1. Reference：RL Lecture 5.pdf (umass.edu)
  2. 要解决的问题
    1. 在Model-free的场景下，习得一个episodic MDP模型的Value function的最大值 $V_{s_t}$ 和最优策略 $\pi_*(s)$ 。
  3. 根本思想是什么
    1. MC prediction: 根据state-Value function预测某个Policy在某个状态下的Value最大值。
    2. MC control：the task that is finding the optimal policy that maximize the value function by alternating between policy evaluation and policy improvements.
  4. 算法流程
    1. MC Evaluation
      1. image-20231008161837614
    2. MC control
      1. image-20231008161904221
  5. 举例说明

21点游戏

  • Objective: having your card sum greater than the dealers without exceeding 21.
  • States
    • current sum
    • dealer’s showing card
    • Do i have usable ace
  • Reward
    • +1 wining, 0 draw, -1 losing
  • Actions
    • Stick(stoping receiving cards),
    • hit(receive another card)
  • Policy
    • Stick if sum is 20/21, else hit.

MC evaluation: 根据以上建模可以写一个MC Evaluation算法来确定这个Policy的Value是多少。

MC Control: 以上述Policy作为初始Policy，随后在某个states下，以$\epsilon$ 的概率选择更新为一个mean(reward)更大的策略，例如更新策略为在sum为16且有ace的情况下应该stick。

  1. 为什么该算法可以解决问题

通过MC Evaluation的迭代，计算每个episode的State Value function就能获得最大值。通过MC Control的迭代，在每个episode以一定概率选择Reward mean更高的Policy，可以获得最大Policy和最大的State Value。

  1. 优劣势
  2. 举例给人听

Policy Gradient

找到一个Policy gradient estimator并把这个estimator放到stochastic gradient ascent算法中进行迭代。

一个非常常见的estimator长这样。

\[\hat{g}=\hat{\mathbb{E}}_t\left[\nabla_\theta \log \pi_\theta\left(a_t \mid s_t\right) \hat{A}_t\right]\]

计算gradient的时候直接对estimator求导。

  1. 为什么这个方法非常方便？
    1. 因为在代码里面，$\log \pi_\theta（a_t \mid s_t)$ 就是所有Token的log probabilities，大语言模型本质都是在预测下一个Token。在计算的时候，estimator的最优值可以直接通过求导得到。
    2. estimator有很多自动求解器，非常方便。
  2. 为什么这个方法有问题？
    1. 这个过程中有需要random sample，对sample之后的结果求导本身是无法解释的；
    2. 这种方法有可能导致Policy gradient非常大。

Monte Carlo Policy Gradient

算法流程

  1. Start with a random policy that tells you what action to take in a given situation.
  2. Try out this policy by interacting with the environment and see what reward you get at each time step.
  3. After each episode, look at the reward you got at each time step and calculate a return for each step. The return is the sum of all the rewards you received after that time step.
  4. Use these returns to update the policy. The update tells the policy to favor actions that got a higher return, by increasing the probability of taking these actions.
  5. Repeat steps 2-4 for multiple episodes until the policy gets better at the task.
  6. Use this improved policy to perform the intended task in the environment.

优势

  1. Policy-based能够直接优化Policy本身；
  2. 可以处理有随机Action的情况；

缺点

  • Noisy Gradient
  • High variance

Actor-Critic

Reference

[Understanding Actor Critic Methods and A2C by Chris Yoon Towards Data Science](https://towardsdatascience.com/understanding-actor-critic-methods-931b97b6df3f)
  1. 要解决的问题是？

传统的Policy Gradient方法有很大的instability，且训练的时候很难收敛。因此要解决RL中以上的两个难题。

  1. 为什么可以解决问题？

TRPO

针对Policy gradient存在的问题，有人提出了Trust Region Method，简单来说就是加入了一个constraint，目的是为了防止某一次策略更新和上一次的策略收益偏差过大。但看公式本身$\eqref{eq_trpo}$其实和Policy gradient的差别并不大，只是加了一个上次策略作为分母。

\[\begin{array}{ll} \underset{\theta}{\operatorname{maximize}} & \hat{\mathbb{E}}_t\left[\frac{\pi_\theta\left(a_t \mid s_t\right)}{\pi_{\theta_{\text {old }}}\left(a_t \mid s_t\right)} \hat{A}_t\right] \\ \text { subject to } & \hat{\mathbb{E}}_t\left[\operatorname{KL}\left[\pi_{\theta_{\text {old }}}\left(\cdot \mid s_t\right), \pi_\theta\left(\cdot \mid s_t\right)\right]\right] \leq \delta . \end{array} \label{eq_trpo}\]

在实际计算过程中，可以把使用surrogate Objective来代替这个constraint problem，比如下面这个Objective

\[\underset{\theta}{\operatorname{maximize}} \hat{\mathbb{E}}_t\left[\frac{\pi_\theta\left(a_t \mid s_t\right)}{\pi_{\theta_{\text {old }}}\left(a_t \mid s_t\right)} \hat{A}_t- \beta \mathrm{KL}\left[\pi_{\theta_{\text {old }}}\left(\cdot \mid s_t\right), \pi_\theta\left(\cdot \mid s_t\right)\right]\right]\]

直接把constraint作为一个penalty。

最大的问题在于这个$\beta$ 并不好选，实际处理的时候在不同问题上$\beta$ 的选择非常影响结果。

搜索