Flash Attention - 两倍速你的训练过程
- 类别:训练
- 效果:训练时候的上下文长度越长,训练加速的效果越明显。15% end-to-end wall-clock speedup on BERT-large (seq. length 512) compared to the MLPerf 1.1 training speed record, 3× speedup on GPT-2 (seq. length 1K), and 2.4× speedup on long-range arena (seq. length 1K-4K).
核心假设
在Transformer训练的时候,没有根据Attention的计算规律考虑到SRAM(on-chip,通常几十MB),HBM(我们通常说的显存)和DRAM(CPU的内存)之间的读取速度,从而导致了计算速度的瓶颈。
分解原本attention计算方法
原本的attention计算方法对内存的读写主要是以下流程,将QK矩阵从HBM中读取出来,计算S并存储到HBM中,所有attention head计算完成后,再从HBM中读取出来所有矩阵运算softmax,再把最终结果写入HBM。

可以看到,这里存储到内存的中间结果马上又被读取进行计算,因此出发点就是,是否可以减少这里的读取操作呢?
如何减少IO操作?
根据上面的分析,立刻就会提出这个问题:是否可以不把S存储到HBM,但仍旧计算出最终的softmax结果呢?
作者提出了两个方法
- Tiling(平铺):简单来说,使用online softmax算法(根据分块计算结果实时更新softmax结果),把QKV矩阵进行分块,对每一块计算softmax的子项,存储一些必要的中间值(标量),从而得到一个最终的softmax结果。
- Recomputation:在进行反向梯度下降的过程中,需要使用到S和P进行计算,由于没有存储S,P,所以需要进行一些重算。即使增加了一些FLOPs,Flash attention还是快了很多,因为内存的操作更加耗时。
方法细节
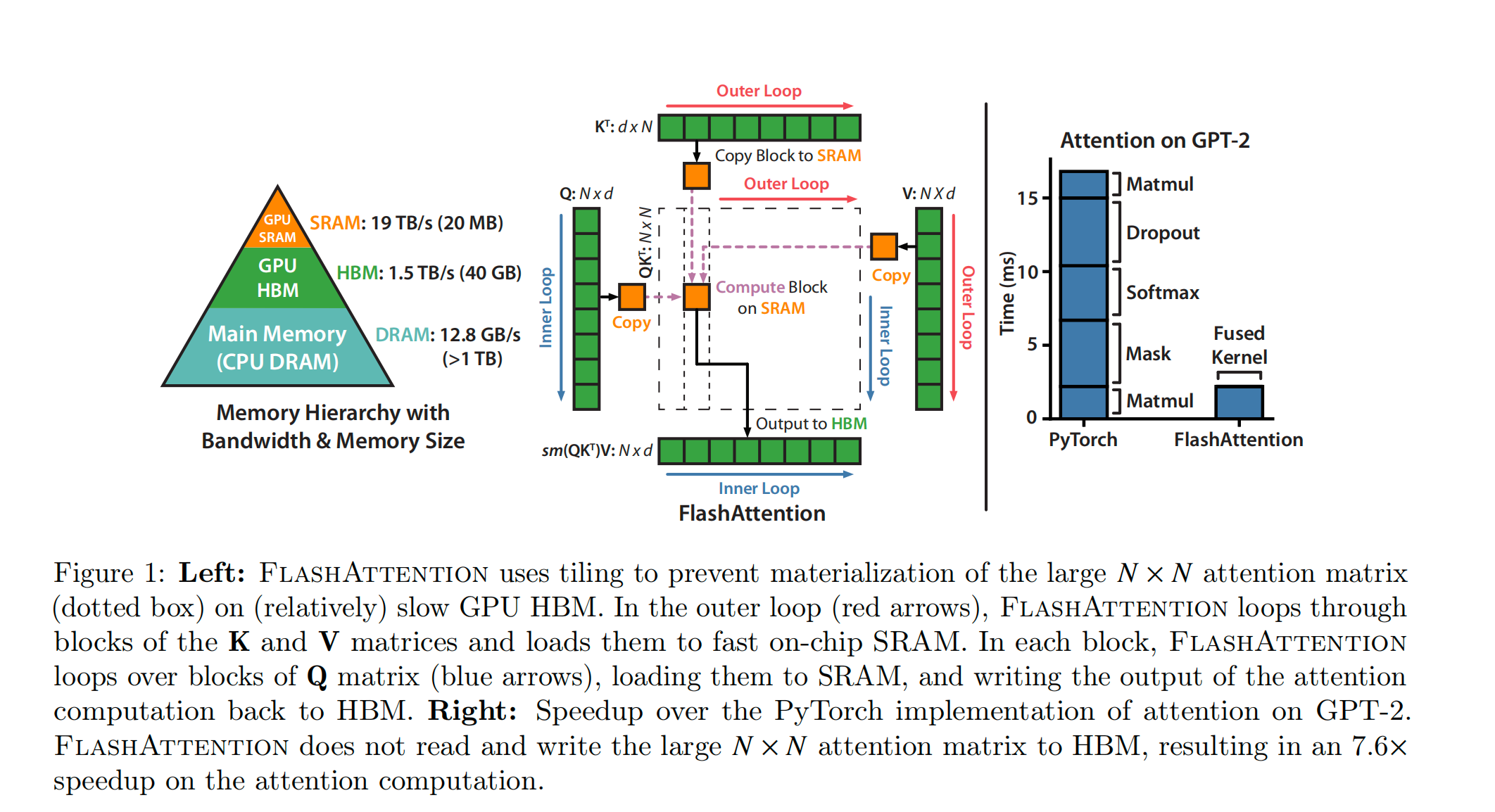
可以看到,inner loop在计算每个attention block的值,并只存储标量到HBM。outer loop则不断将attention矩阵的值拿到内存中。
下面我们看下,recomputation是如何加速的。首先反向传播的时候,dV是很好计算的
\[dv_j = \sum_i P_{ij} do_i = \sum_i \frac{e^{q_i^T k_j}}{L_i} do_i.\]这里我们能看到$L_i$是已经计算并存储过的标量,所以可以直接得到dV。
这里省略部分dQ的推导过程,直接给出结论是
\[dq_i = \sum_j dS_{ij} k_j = \sum_j P_{ij} \left(dP_{ij} - D_i \right) k_j = \sum_j \frac{e^{q_i^T k_j}}{L_i} \left(do_i^T v_j - D_i \right) k_j.\]理论分析

根据standard implementation的结果,可以看出总的访问开销是$4ND+4N^2$,使用flash attention,内循环需要读取整个Q,所以复杂度是$Nd$,外循环决定了内循环的执行次数,而外循环$T_c=\frac{N}{Blocksize}=\frac{4Nd}{M}$,因此整体的复杂度就是$O=\frac{4N^2d^2}{M}$,实际上M的大小通常远大于d,因此相比原来的attention计算空间复杂度是有很大提升的。
总结
Flash attention通过分解attention的计算矩阵,使用online softmax计算方法,从而实现了计算的加速,从结果来看,对GPT-2模型有2-3x的加速效果,尽管在反向传播时还增加了FLOPs。