Algorithms to live by

我觉得很多人应该更熟悉这本书的中文译名，算法之美。看到了微信读书上对于这个译名的评价：为了追求所谓的“信达雅”而没有正确翻译出题目想表达的主题，乍一看还以为是讲算法的，实际上是讲算法在日常生活中的应用的。并且后半部分的翻译好像是为了赶工，看上去并没有针对中国人的表达习惯进行优化，非常像是机翻的，这就导致了后面几章的内容读起来比较晦涩。因此为了避免这个情况，我直接选择读原版的英文版。这反而对于我比较友好，因为上学学算法的时候就是英文教材，很多argot是可以直接代入和理解的，比阅读中文版更能让我理解作者表达的原意。

Regardless of that，这本书讲的还是非常好的。通过算法引申到哪些现实问题其实是这个算法的真实映射，而如果算法本身能够提供解决问题的最优解，那么我们同样可以把这个策略用到我们的生活当中。

Abstract

This book is all about introducing how you can apply algorithms to your daily life decisions to make your life easier.

Optimal stopping

“the optimal solution takes the form of what we’ll call the Look-Then-Leap Rule: You set a predetermined amount of time for “looking”—that is, exploring your options, gathering data—in which you categorically don’t choose anyone, no matter how impressive. After that point, you enter the “leap” phase, prepared to instantly commit to anyone who outshines the best applicant you saw in the look phase.”

This principle applies to any situation where you get a series of offers and pay a cost to seek or wait for the next.

Explore/exploit

A situation where you don’t know which restaurant to go to, the existing known good or undiscovered ones.

一个简单的策略

Win-Stay, Lose-Shift algorithm: choose an arm at random, and keep pulling it as long as it keeps paying off. If the arm doesn’t pay off after a particular pull, then switch to the other one. Although this simple strategy is far from a complete solution, Robbins proved in 1952 that it performs reliably better than chance.

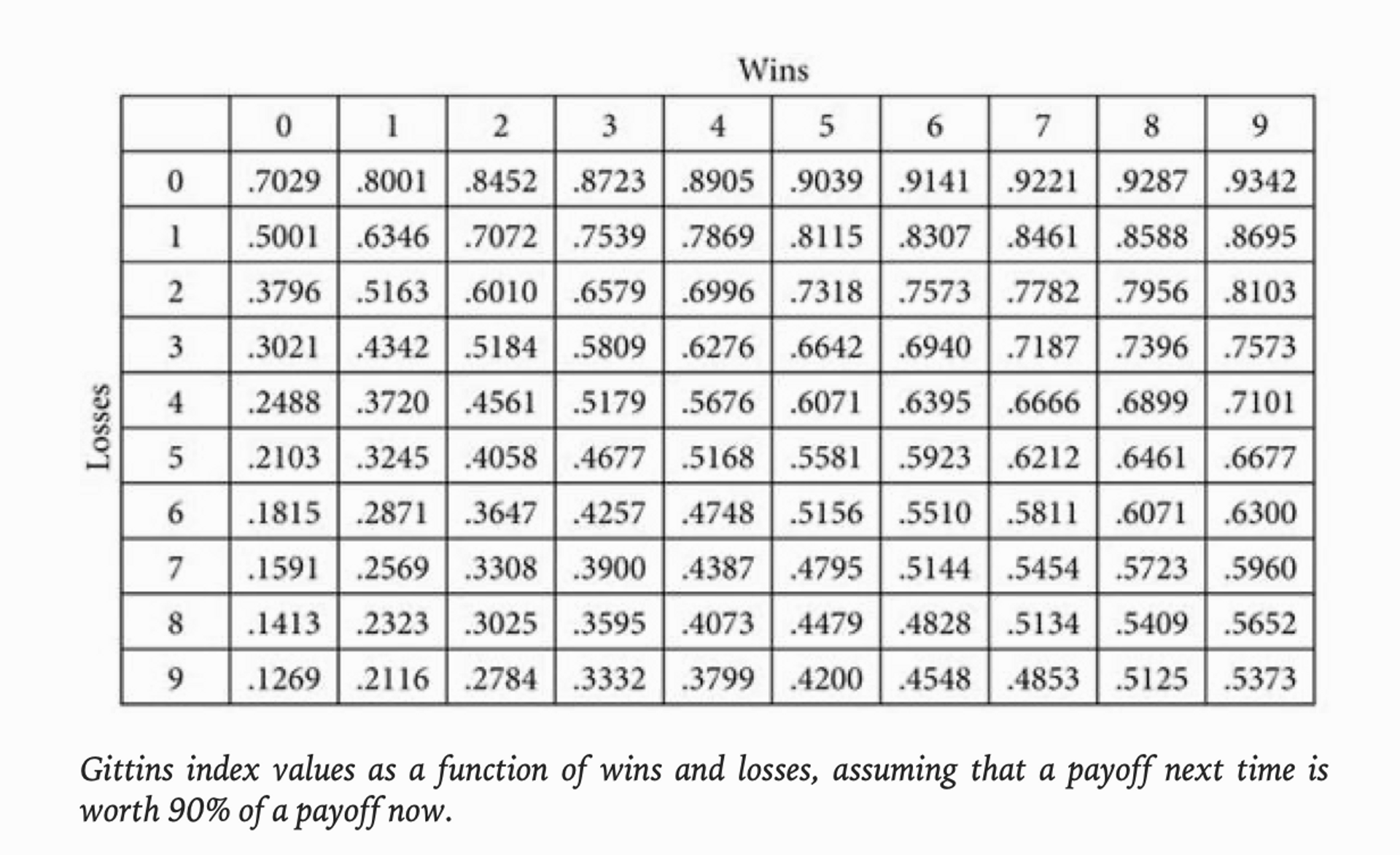
The Gittins index

假设每次探索成功后，得到结果满意程度是上次的90%。那么就会有下面这张表。

cache

Cache在生活中会有一些可以优化工作流的场景，比如电脑桌面程序和网页，保留哪些，关掉哪些。哪些是可以保存在收藏夹的，哪些是可以不在收藏夹但是可以通过两个动作打开的。

这么看的话可以把收藏夹问题抽象成一个多级缓存问题。对于这个处理原则可以是

1. 哪些是最经常打开的？
2. 哪些频率略低，可以花时间寻找的？
3. 哪些可以直接放到文档里面，用到了再去找文档的？

First, when you are deciding what to keep and what to throw away, LRU is potentially a good principle to use

“Second, exploit geography. Make sure things are in whatever cache is closest to the place where they’re typically used.”

难以想象，其实社会对于事件的遗忘程度也是一个艾宾浩斯曲线。

Scheduling

基本概念

1. DDL优先：当你的事情没有重要性排序的时候，你只需要将每一个事情按照到达次序处理，找到快要DDL的事情来做就行。
2. Thrashing，当你的事情有优先级排序的时候，很多事情又同时在做，就会崩溃，你发现其实一直在做context swtich，最后其实什么也没做，在外界看来，这样甚至成了拖延症。
3. 最小时间分片。操作系统实际上有个最小分片，小于这个分片，系统除了不断做context swtich，什么计算任务也无法完成，所以这个最小时间分片是无法继续分割的，必须做完才能做另一个任务。

Takeaway

1. 确定自己的最小处理时间分片。在一个分片内，尽量只做一件事。“The moral is that you should try to stay on a single task as long as possible without decreasing your responsiveness below the minimum acceptable limit.”
2. Interrupt coalesce. 把给你的中断尽可能合并，比如统一回复邮件。
3. 对于概念2，可以随机处理事情，而不需要一直卡着优先级排序处理，否则在计算优先级这里又需要花很多时间。

Bayes Rule

1. How to predict the probabilities if it happens only once?
   1. “Count the number of times it has happened in the past plus one, then divide by the number of opportunities plus two. ” da

人们总是会对最近发生的事情记忆更深，因此，往往会给最近的事情加更多的权重，这会让本来有可能预测准的事情不准。因此要谨慎对待类似的事情。

Overfitting

顾名思义，这章基本上就是在讲，如何能通过正则化，噪声等来避免过拟合带来的影响。

“how early to stop depends on the gap between what you can measure and what really matters.”

Relaxation

这章有个很有意思的观点，relaxation在数学里面的典型代表就是Lagrangian方法，把所有的constraints都当成优化函数的一部分，成为一个新的函数。即利用限制条件来修正优化函数，通过限制条件的最终数值，求得参数值，就能得到原函数的最优解。

类似的事情就是在生活中，我们面对很多选择的时候会受到很多限制条件的束缚。例如必须要工资在多少以上的，工作的位置必须在什么地方，等等。但如果目标是最合适自己的工作，就可以问自己，如果所有工作的工资都一样，我会选择什么？

实际上，在很多时候一个合适的放缩能找到的答案就是最优解了。

Randomness

随机，有时候是解决untractable问题的良药。比方说公私钥机制里面的大整数分解问题，本身找到一个数字是哪两个质数的乘积是一个只能穷举的算法，但是如果你可以接受一些错误率，用一些随机的方法，可以在错误率很小的情况下进行验证。

Networking

Networking里面的慢启动和拥塞避免算法竟然可以映射到职场里！

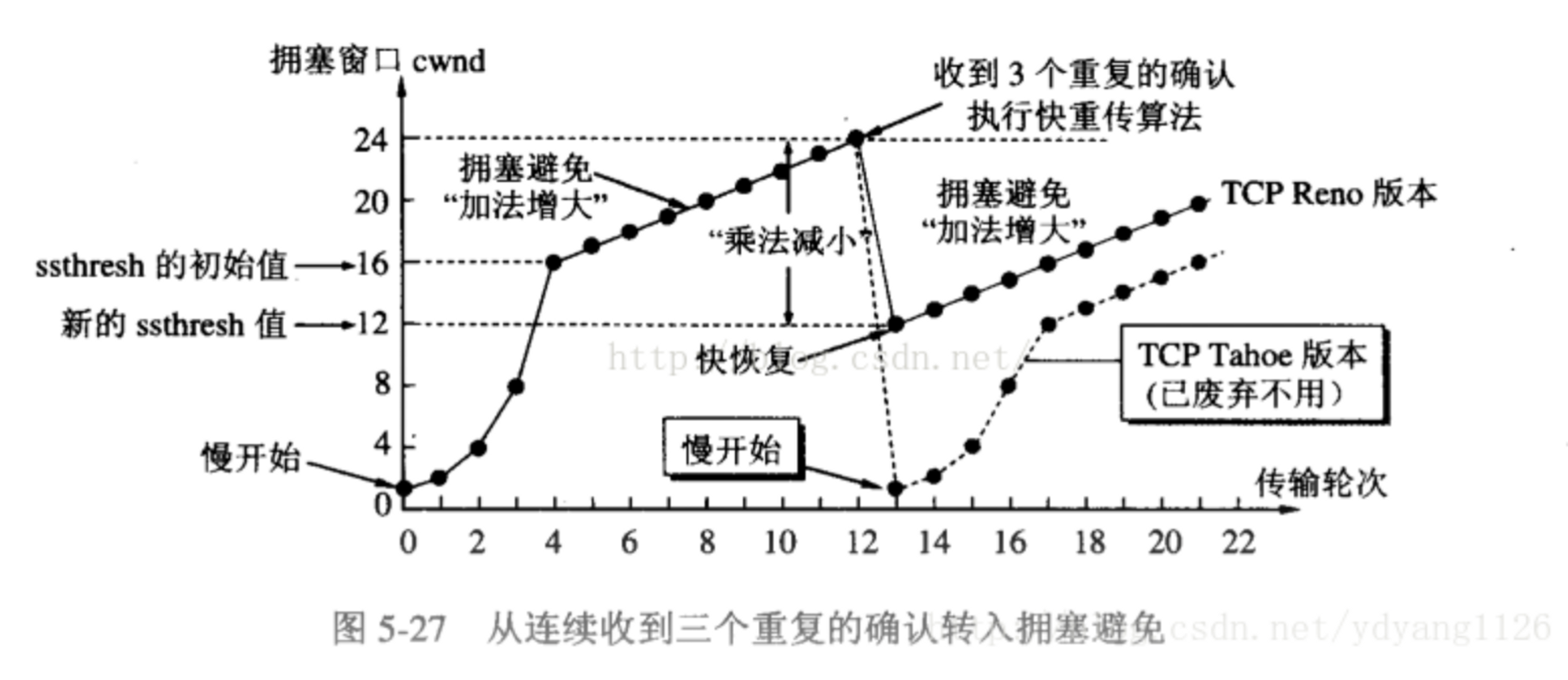
考虑这个拥塞避免算法的本质是什么：在不知道对面capacity的情况下，怎么能快速试出来？

在工作中，作为领导，不知道这个人上限是什么的情况下，怎么能快速试出来？

快速指数级升职，直到他无法做好目前的工作。然后降到当前职级的一半（或者工作负载的一半）然后再线性提升。

Game theory

在博弈论里，有一些假设就是每个人都是理性人，大家会做出在当前对自己局面最好的选择。

尽管比较难以接受，即使我们现在全部都变成自动驾驶，有成熟的算法来帮我们规划，在最好的情况下，堵车只能比现在少$\frac{1}{3}$。

在一些不行的Game里面，无论一个人怎么努力，最好的结局是也只是到达一个这个游戏的均衡点。作者用了黑五商店开门举了例子，以往黑五商场开门时间都是早晨8点。但是突然商场A说自己改成凌晨0点开门，对于其他商场来说，必须也在0点开门，这样才能保证销量。因此所有的商场都在0点开门，而谁也没有多挣到钱。这就是一个bad Game。

因此给我们的启示是

“If changing strategies doesn’t help, you can try to change the game. And if that’s not possible, you can at least exercise some control about which games you choose to play. The road to hell is paved with intractable recursions, bad equilibria, and information cascades. Seek out games where honesty is the dominant strategy. Then just be yourself.”