防止OOM的利器:Gradient checkpointing
- 类别:训练
- 效果:Gradient checkpointing在能够容纳10x模型大小不OOM的情况下,只增加20%的训练时间。是一个tradeoff训练时间且比较高效的方法。
Existing Gap
大家训练的时候都遇到过OOM的问题,这里面有很大一部分原因是需要存储运算的中间结果Activations。在Mixed Precision Training里提到过,我们再以Adamw优化器为例,回顾下训练时候总的内存占用。
训练时内存保存的状态是,Activation,Gradients和Weights。我们假设训练的BatchSize是$B$,模型的大小是$N$,模型的层数是$L$。那么,Adam训练时需要存储
- Gradients:需要存储Gradients的一阶估计和二阶估计,总占用内存是$2N$。
- Activations:计算每一层的时候需要用到$\sum_{i = 1}^{L} 4\times B\times n_{i}$内存
- Weights:$N$大小的内存。
核心假设
能否使用时间换空间,少存储一些activations呢?这就是Gradient Checkpointing的核心思路。
具体方法
在一个有L层的Feedforward的网络中,Gradients的计算网络是这样表示的:
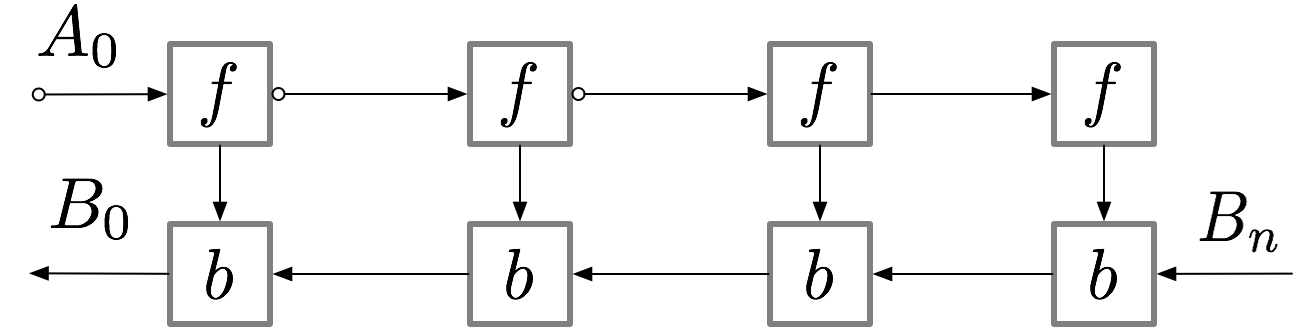
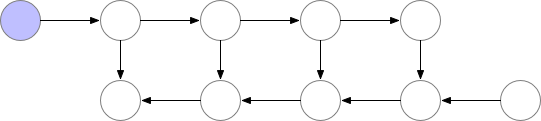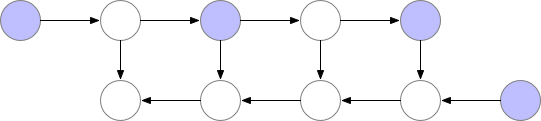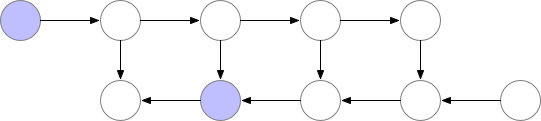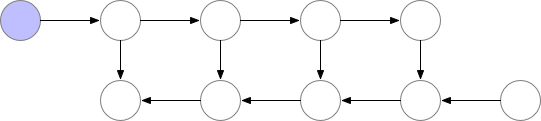
神经网络层的激活对应于标有 f 的节点。在前向传播期间,所有这些节点按顺序进行评估。损失相对于这些层的激活和参数的梯度由标有 b 的节点表示。在反向传播期间,所有这些节点按相反的顺序进行评估。计算 b 节点需要为 f 节点获得的结果,因此在前向传播后,所有 f 节点都保留在内存中。只有当反向传播进展到足以计算出 f 节点的所有依赖项或子项时,它才能从内存中删除。这意味着简单反向传播所需的内存随神经网络层数 n 线性增长。下面是这些节点的计算顺序。紫色阴影圆圈表示在任何给定时间需要保留在内存中的节点。
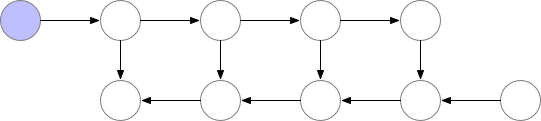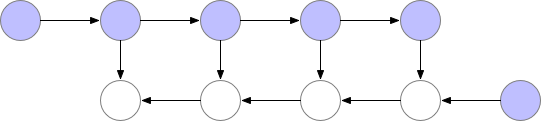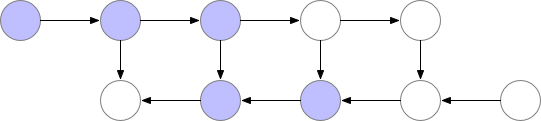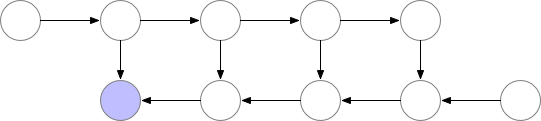
如上文所述,简单的反向传播在计算方面是最优的:它每个节点仅计算一次。然而,如果我们愿意重新计算节点,我们可能会节省大量内存。例如,我们可能每次需要时都简单地从正向传播重新计算每个节点。执行顺序和使用的内存情况如下:
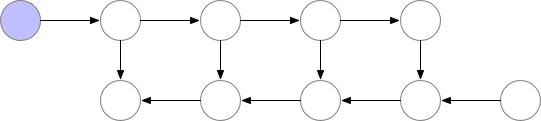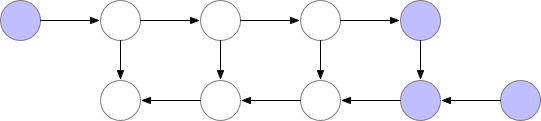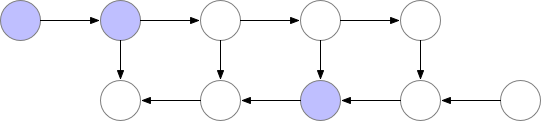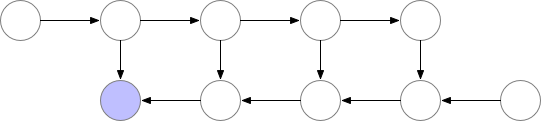
使用这种策略,在我们的图中计算梯度所需的内存对于神经网络层数 n 是恒定的,这在内存方面是最优的。然而,请注意,现在节点评估的数量与$n^2$成比例,而之前是与 n 成比例:n 个节点中的每一个都要重新计算大约 n 次。因此,对于深度网络,计算图的评估速度会变得慢很多,这使得这种方法在深度学习中不切实际。为了在内存和计算之间取得平衡,我们需要想出一种策略,允许节点重新计算,但不要太频繁。我们在这里使用的策略是将神经网络激活的一个子集标记为检查点节点。
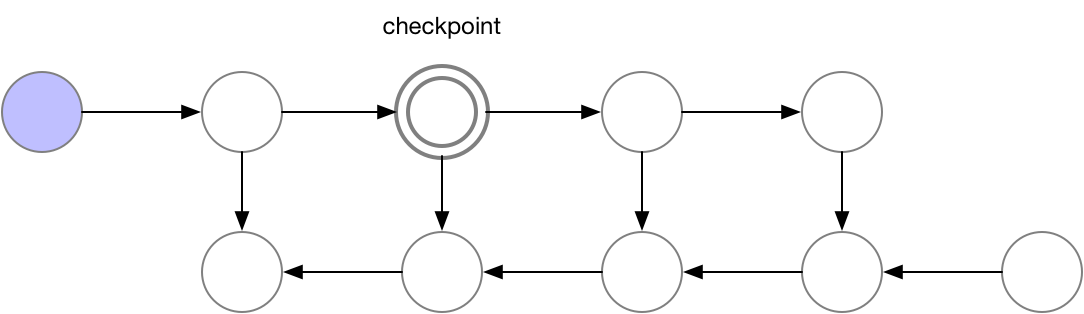
对于我们示例中的简单前馈网络,最佳选择是将每第 sqrt(n) 个节点标记为检查点。这样,检查点节点的数量和检查点之间的节点数量都在 sqrt(n) 的数量级上,这意味着现在所需的内存也与我们网络中的层数的平方根成比例。由于每个节点最多重新计算一次,此策略所需的额外计算相当于通过网络的一次前向传递。对于包含关节点(单节点图形分隔符)的图形,可以使用 sqrt(n) 策略自动选择检查点,为前馈网络提供 sqrt(n) 的内存使用量。对于仅包含多节点图形分隔符的更一般的图形,我们的检查点反向传播的实现仍然有效,但我们目前要求用户手动选择检查点。
总结
在每个Activation计算的时候,只选取其中的Sqrt(n)子集作为需要保存的,其他都在反向传播时候重新计算,这样能够较为有效的节省内存。
后记:Gradient Accumulation是什么
Gradient Accumulation主要解决的问题是增大batch_size,即不在计算每个batch后立即用Gradients更新权重,而是在攒了几个batch的Gradients之后求和,再对模型权重进行更新。好处是某些训练是对batch_size有要求,这个方法可以解决该问题,但不好的地方是可能加长训练时间并且收敛较慢。