介绍
控制算法主要用于控制系统状态,通常情况下输入数据和系统状态会不断改变,控制算法能够根据这些改变动态调整当前系统状态,使得当前系统状态与输出能够和目标状态与输出接近。
例如想制作一个恒温水壶,想让这个水壶的温度维持在60°C左右,此时首先需要将水温升到60°C附近,然后根据环境温度、水温等状态使水的温度尽可能维持在60°C。
算法分类
PID算法
根据介绍中提到的目标,PID(Proportion, Integral, Derivative)算法的工作流程可以总结为图1所示,
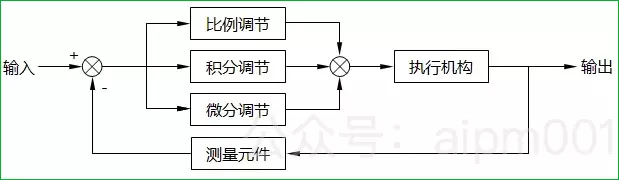
图1:PID算法控制过程
PID的数学表达:
\[U(t) = kp(err(t)) + \frac{1}{T_1} \int err(t)\ dt + \frac{T_Dderr(t)}{dt}\]其中第二项是积分(integral),第三项是微分(derivative)。
补充知识点,积分和微分。积分:可以参考图2(左),计算当前函数曲线和坐标轴围成的面积大小。主要作用,组合许多无穷小的量,形成面积、体积等计算量[2]。微分:参考图2(右),计算当前函数自变量每变化一点,因变量对自变量变化的敏感程度(In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value)[3]。
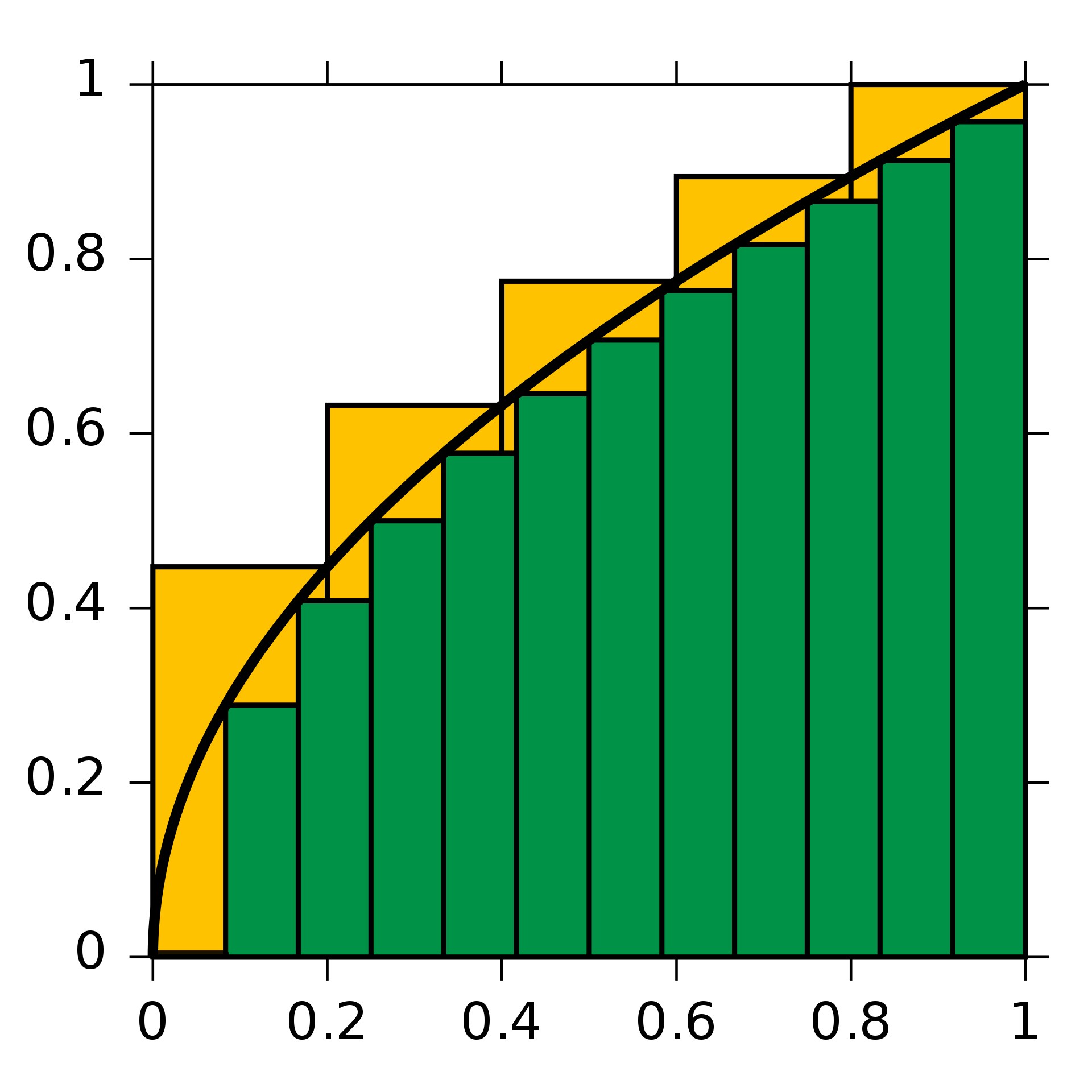

图2: (左)积分图形表示。(右)微分的图形表示,可以看作一维函数的切线。
在PID中,后两项可以看作在逼近目标函数的时候进行微调,在我们控制水温的例子中,就是在接近60°C的时候进行调整的项。
在实际应用中,一般来说$err(t)$是确定的,就是实际应用中的偏差函数,所以比较难的就是确定这三个项的系数。
MPC算法
MPC算法介绍
在介绍MPC算法之前,先介绍两个概念,开环控制和闭环控制系统[5]。
| 名称 | 定义 |
|---|---|
| 开环控制 | 开环控制是指无反馈信息的系统控制方式。当操作者启动系统,使之进入运行状态后,系统将操作者的指令一次性输向受控对象。 开环控制的特点是系统的输出量不会对系统的控制作用发生影响,不具备自动修正的能力,即不存在反馈环节。此外,由于系统不存在反馈,所以开环控制一般是在瞬间完成。 |
| 闭环控制 | 闭环控制是指有反馈信息的系统控制方式。输出量直接或间接反馈到输入端形成闭环、参与控制,在输出端和输入端之间存在反馈回路,输出量对控制过程有直接影响。通俗来说,若存在干扰,导致系统实际输出产生偏差,系统可以利用负反馈产生的偏差所取得的控制作用再去消除偏差,使系统输出量恢复到期望值上。此外,由于反馈存在,闭环控制一定会持续一定的时间 |
模型预测控制(Model Predictive Control)指一类算法,周期性基于当前帧测量信息在线求解一个有限时间开环优化问题,并将结果的前部分控制序列作用于被控对象。
MPC算法最主要的优势是,能够优化当前的最小时间周期,并且还能考虑到未来的时间周期(The main advantage of MPC is the fact that it allows the current timeslot to be optimized, while keeping future timeslots in account.)
在实际应用中,往往需要控制的参数非常多,可能同时有很多PID模型在运行,这些参数之间往往也不相互独立,因此PID算法在动态性较强的系统中,往往存在时延较大,阶数较高等问题。如图3所示,在MIMO(Multi Input Multi Output)系统中,每一个子系统需要单独设置控制器,系统越大则越难以设计。相比于PID算法,MPC算法能对动态系统有更好的控制性。
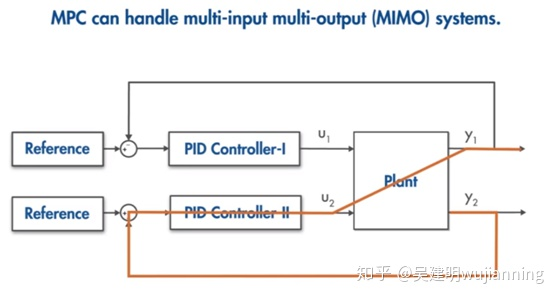
图3:PID控制器设计在MIMO情况下存在参数多难以设计的问题。
MPC在Wiki上的定义:
MPC is based on iterative, finite-horizon optimization of a plant model. At time $t$ the current plant state is sampled and a cost minimizing control strategy is computed (via a numerical minimization algorithm) for a relatively short time horizon in the future: $[ t , t + T ]$. Specifically, an online or on-the-fly calculation is used to explore state trajectories that emanate from the current state and find (via the solution of Euler–Lagrange equations) a cost-minimizing control strategy until time $t + T$. Only the first step of the control strategy is implemented, then the plant state is sampled again and the calculations are repeated starting from the new current state, yielding a new control and new predicted state path. The prediction horizon keeps being shifted forward and for this reason MPC is also called receding horizon control. Although this approach is not optimal, in practice it has given very good results. Much academic research has been done to find fast methods of solution of Euler–Lagrange type equations, to understand the global stability properties of MPC’s local optimization, and in general to improve the MPC method.
简单来说,就是对于一个MPC算法,通过以下步骤对系统进行控制
- 构建一个系统持续运行的动态模型;
- 定义一个基于下一个时间窗口的损失函数$J$;
- 对于给定的输入$u$,使用某种优化算法对损失函数$J$进行优化。
算法的具体流程可以参考我画的这两页PPT已经录制的视频。
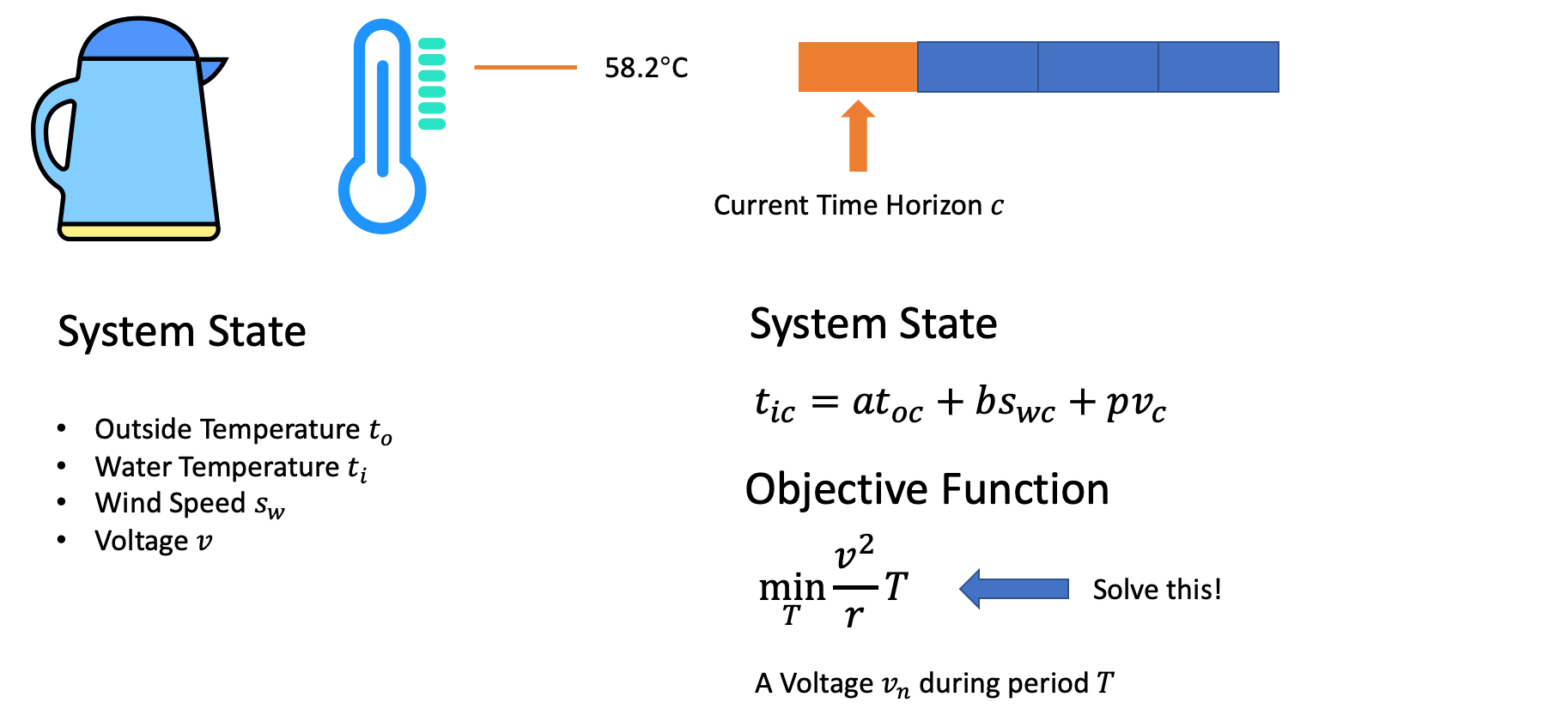
图4:MPC算法初始流程
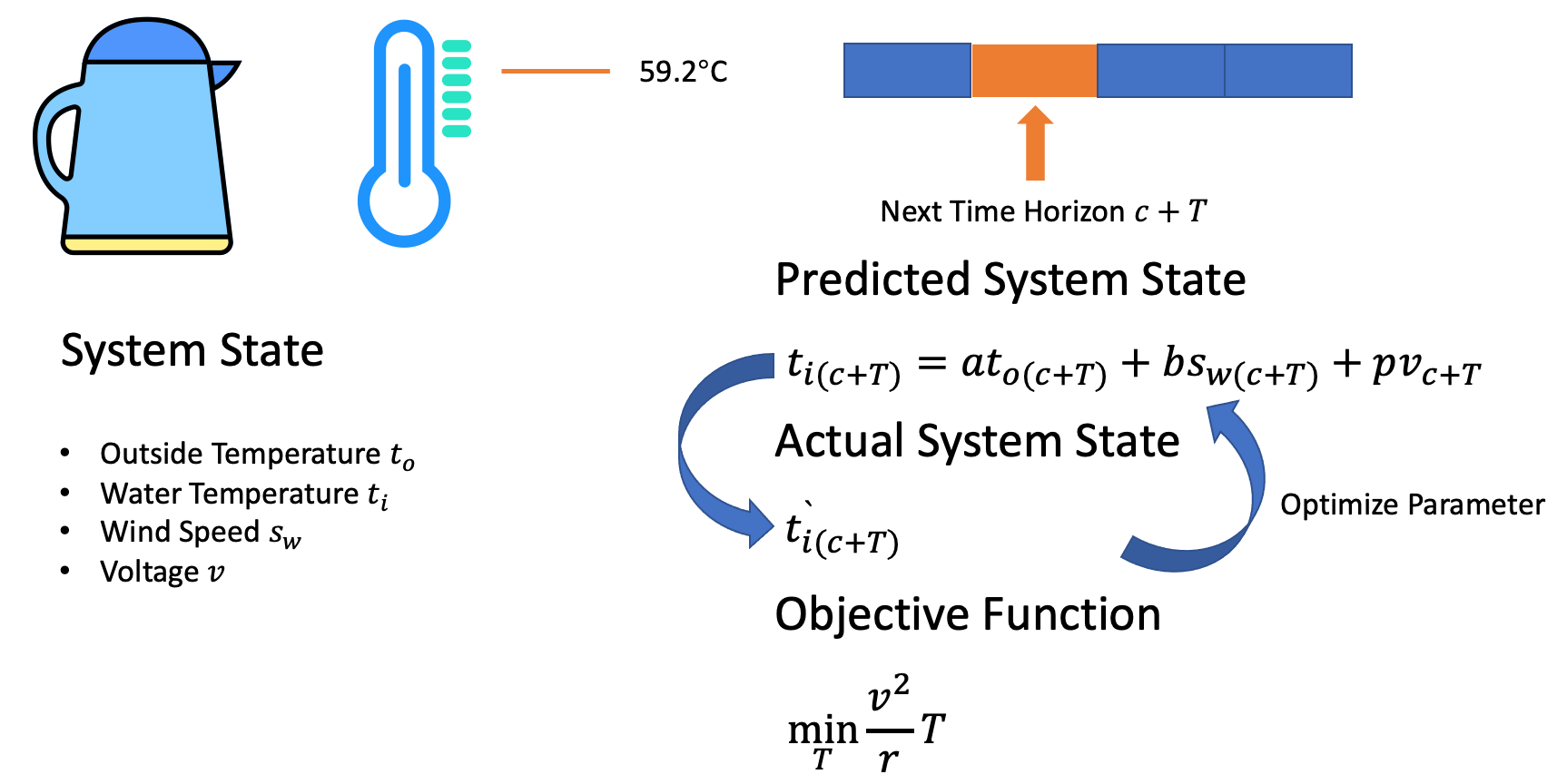
图5:MPC算法第二部流程
视频1:MPC算法讲解
MPC算法调参
根据以上介绍可以得到,如果需要优化MPC模型,可以优化的参数包括:
- 采样周期:多久对系统状态进行一次观测;
- 预测范围(time Horizon):预测多久以后的系统状态;
- 状态转移方程:预测系统状态和当前系统状态的差值。
可能还包含别的需要优化的参数,需要具体问题具体分析。
更优原因
相比于PID算法,MPC算法的优势在于,可以整体Model所有参数,整合成系统状态,而不需要对每一个子系统进行单独的模型建立和优化,所以对于动态、复杂的系统适应性更好。
优劣比较
| 算法名称 | 优点 | 缺点 |
|---|---|---|
| PID | 1. 更接近最优:调整策略就是目标,更加直接。 2. 实时性尚可. |
1. 高延迟:需要反应时间很长,但是算的很快; 2. MIMO系统处理能力差。 |
| MPC | 1. 可以处理延迟:MPC采取了一个折中策略,不是只考虑当前状态,而是考虑未来有限时间域的状态。 2. 可处理MIMO系统。 3. 可以处理多约束。 |
1. 一定程度牺牲了最优性 2. 计算量较大:每次产生策略都需要解一个优化问题。 3. 实时性不高:计算量大则需要的时间长,因此虽然可以处理未来时间段的,但是计算时间也更长。 |
Take Away Notes
本文主要介绍了两种控制算法,PID算法通过调整比例、微分和积分来控制系统状态,MPC算法通过对系统状态建模,动态调整下一个时间窗口的时长和状态转移方程的参数,在某个时间解决优化问题来达到控制的目的。